Simple calculations on a reciprocal roof
-

Model of a reciprocal roof, made from natural materials. Despite the differences in diameter, a neat result is obtained.
- A reciprocal roof is a kind of roof in which every rafter is supported by the previous one, resulting in a strong, self-supporting construction. But what will be the angle of my reciprocal roof? That’s for many amateur builders generally a process of trial and error. However, it is rather easy to calculate this roof angle. Grab a calculator and join in.
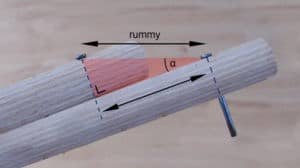
Usually a reciprocal frame will be covered in vegetation, so a relatively small angle is desired. Only two variables have influence on the angle: the thickness of the timber and the so called rummy. The rummy is the distance between two consecutive places where two poles meet each other, measured horizontally. The picture will clarify. The smaller the rummy, the larger the roof’s inclination. So, by selecting enough length of the rummy, you will be ensured of a limited roof angle.
- The top arrow represents the rummy, the bottom arrow the distance between two mounting points
- Depicts same as previous picture, slightly different camera angle
- Alpha is a good approximation of the roof angle
The three pictures above further clarify the geometry of a reciprocal roof. Alpha represents approximately the roof angle of the entire reciprocal construction. The trick is to find alpha by applying some basic goniometry on the right-angled triangle. We’ll get back to that in a moment.

With as little as three poles a reciprocal frame can be constructed. Note that the central opening has the same number of corners as there are poles.
The circumference of the central opening is obviously dependent on the size of the rummy and the number of poles. The length of the contour is simply the rummy times the number of poles. The diameter of the central opening is more or less the circumference divided by π (3,1415). As the number of poles increases this approximation improves, because the central opening approaches a circle more and more. In the most extreme case the reciprocal frame consists of just three poles which leads to a triangular central opening. However, the diameter of even a hexagon is well approximated by taking six times the rummy and divide the result with π.
When using a high number of poles for a reciprocal frame, the central opening will probably get to large. Decreasing the rummy is not an option either, because this will increase the roof angle. The best option will then be to make a notch every time two poles meet. The effective diameter will thus be reduced locally and the roof angle will decrease subsequently. Still the key question remains: what will be the roof angle? Get your calculator, enter the (effective) pole diameter and divide by the rummy. Now take from the result the inverse sine (arcsin of sin-1) and there you have it: the roof angle in degrees. Make sure your calculator is actually set on degrees (deg). Alternatively, you can also use this small Excel sheet.
Although the number of poles influences the size of the central opening, it hardly changes the roof angle. It could change in the order of a degree because the poles will meet slightly different at varying numbers of poles, but that’s it. The roof angle is also not affected by the length of the poles.
Other properties of a reciprocal roof
The load of a reciprocal roof on the wall below is definitely favourable. Once the roof has settled in its definitive position, the weight only works vertically on the wall. So, the wall does not encounter outwards directed forces.
In the middle of the construction each pole rests on the previous one. Even without any fixing a reciprocal frame can be stable. Especially when using a larger number of poles the frame will remain standing. In actual construction a sturdy fixation is recommended, but it illustrates the intrinsic stability of a reciprocal frame.
Many reciprocal roofs are build with round wood. Posts are stronger than square or rectangular timber. An important advantage of round wood is that the fiber structure is nowhere cut. This yields more strength at the same weight.




How do you calculate the diameter of a pole? For example for a ground surface of 60 m2, hexagonal shaped construction.
This depends on a lot of factors. The kind of wood, the number of rafters. Rule of thumb: de diameter should be 1/20 of the length from wall to the point where the pole / rafter meets other rafters in the middle. So, is this distance is 4 meters, the diameter of the pole should be 4 / 20 = 0.2 metres or 200 mm. However, in the case of a vegetation roof, larger diameters may be needed.
Good article. I have a 20′ diameter octagon. I am using your excel sheet to calculate the diameter of the center octagon using 8 rafters (4″x4″)I would like it around 3-4′, but I am weary of the roof angle, as I live in a heavy snow load area.
I would like a larger roof angle, with a 3-4′ opening using 8 rafters, but cant seem to make it work on the spreadsheet?
Also, I am curious how to determine the length of the rafter?
Thanks,
Well, the roof angle follows solely from the rummy and the diameter of the rafters. So, a certain roof opening combined with a certain pole diameter will give a certain roof pitch. A steeper roof angle will give a smaller central opening. Let me know if you need any help with this. And sorry for the late reply!
Hi, i would like to make me sure about process of callculation.
If i want to have 30° angel of my roof… i must know diameter of pole and from this i can calculate the rummy. Now from the rummy and number of poles i can calculate diameter of roof opening. Is it correct way of callculation?
I still missing relation bettwen number of poles and roof angel – is it there relation or not? Second thing which i dont uderstand is seting heigh of first pole during construction process. Can you write me something about this?
Thanks a lot, Ondřej
Hi, I plan to make a reciprocal roof for a pithouse. I use ‘Robinia pseudoacacia’ round wood, I plan 8 poles for a 6meter wide pit, I want secondary poles to cover the roof and do intensive live roof (12cm or more). You know to help me in what diameter main poles I need and how lenght to do for 1meter central hole? I plan to sit 50cm from poles on the ground. And whag angle is needed at joints? Thanks if you help me! (greetings from hungary)
Hello, I would like to know if this type of roof can withstand a cyclone. I live in an area concerned by this kind of phenomena. I am looking for links to understand how to do it! In French if possible!
Thanks for the article!
Sorry, I don’t speak French…
A reciprocal roof in itself is not better or stronger during a cyclone. However, the round shape and the lack of vertical parts does help in strong winds. Strengthening the frame as a whole can improve its characteristics in strong winds. Anchoring everything well is another point of attention. But these are just a few of the aspects you need to take into account. I would say a local expert best have a look at the plans!
We are about to break ground in may and I was thinking of doing a 10ft high earthbag roundhouse at 24ft diameter. I live in the 4 corners region in Colorado and this winter we had a lot of snow, so I would want the roof angle somewhat steep to shed that snow. I’ve got good access to a few different local mills so I can get any diameter poles. How many rafters would you recommend and what diameter pole? Thank you very much for posting this. We were thinking of an easier roof but this is our dream so it might as well be love to look at.
Would it be possible to safely use reclaimed telegraph poles for a reciprocal grass roof?
Hi! We are building an 8 m diameter earthbag house. We have rafters for the r.roof of 4.1 m and 15 cm in diameter. Are the poles long enough,and can we go with 13 piece? Thanks for help
Who can help me calculate dimensions of round timber for reciprocal roof construction with a diameter of 11 meters with 18 rafters and piles. Roofing weighing 100 kg / square meter?
Thanks so much for information! I am in need of a studio space to do my crafting in and want try a reciprocal roof . Going to living roof workshop with Sigi Koko in October and would like to combine the two concepts 😊 Appreciate you sharing the math involved in an understandable format!
Can you aim me toward information on the load bearing issues with living roof on reciprocal? Thanks so much
Hi I can’t seem to find any information about using black bamboo for a reciprocal roof. Just a small 15 1/2 foot diameter greenhouse. However the approximations equal 8” and bamboo doesn’t do 8″ diameters but the tensil strength of bamboo is equal to steel. So it seems like it should be possible with less than 8″ diameter bamboo.
Specific to bamboo I should probably tie it togeather to maintain strength rather than drill holes through it but I’m not sure what to use to tie the bamboo poles in place? Straps? Flat rope? Any ideas?
No bamboo in the Netherlands, so I can’t really give any advice. Anybody else any ideas?
Hi Daniel,
Would it be possible to get a copy of the spreadsheet for reciprocal roof calcs?
I’m trying to figure out the rummy needed for a roof with 9″ diameter (circular) beams, 20 deg roof slope, 16.2919′ outer radius.
Thanks in advance,
Lawrence
Hi, didn’t the link in the article to the sheet work properly?
Dear Daniel, I plan to build my own house soon with a reciprocal roof (max 40m2), and i am wondering if it is possible to make it oval instead of round, that would be more practical in terms of space use. I looked around on internet and i see only round roofs, maybe an oval roof would need to keep a pole in the middle? What do you think? Thank you very much 🙂
Hi Gregory, I think it’s possible, but I recommend to make a model first. I discovered some weird shapes and forms working on a small scale!
I’m planning an oval footprint for my build, with a round reciprocal roof. This will need the walls to vary in height to be stable, so that no other roof support is necessary. I think by using the excel sheet here to find the roof pitch, it will then be possible to calculate the difference in wall height required to support each rafter at its point of contact with the supporting wall. I think I’ll make a scale model to check it works out though!
Hello! Great website thank you.
We want to do built a octogone (12m diameter) with a reciprocal frame roof.
What material would you use for the roof itself?
Thank you 🙏
Hey Guys, its that time of year again whem hoping to get the recirpocal roof on my greenhouse. Never heard back from Daniel and looking for a contact with an engineer who can get me some drawings. Please let me know if you made any progress with your projects and if youi require drawings with your muni. I will do the same! Thanks
Oops, sorry for not replying. Are there specific questions at the moment?
Hey Daniel, thanks for replying. We have an imperfect oval, 29ft diameter and 25 ft diameter that intersect at the middle. The rafters at the longer ends will need be approx 20ft long to reach the middle for a reciprocal roof. I have an engineer friend who speculated we will need 2×12, 2 plis to span that distance. We live in Western Canada so snow load is a factor but the sheer size and mass of 10, 3 plis 2×12’s would seem to make the rummy pretty much impossible. What am I missing?
First of all, what is plis…?
Wouldn’t the rummy be possible with the correct cutout? Like this: https://i.pinimg.com/564x/13/e6/7d/13e67d4e473ca1f227d67ea3c643ef0e.jpg
Bloody busy at the moment, but I’d love to make a simple model at the correct scale. Do you have a website or something with pictures?
Does anyone know if it’s possible to swap out a primary pole from a reciprocating roof??
Brilliant article thanks. Two questions. I don’t understand why there is no lateral thrust against the walls. In rectangular structures you neeed some form of cross tie. Is it the spiral nature of the roof that does this?
How do you fasten round poles to the walls?
Thanks.
Hey Daniel. Great thread and I’m glad I found it. I am building an oval green house with 10 posts. The two longest distances are 30 feet, and the cross distance is about 25 feet. I am using 6×6 round poles for the 10 uprights and thinking of using 3+” fence rails for the reciprocal roof. I have a few questions but first and foremost what do I need to be aware of using a reciprocal roof with an oval? Will the wooden fence rails suffice considering I am in a high snow fall area in we set er. Canada? Any additional advice or director would be much appreciated! Regards, Brad. Stay safe everyone.
Hey Daniel, been doing some research and calculate a roughly 18 ft span on each post would require about a 10.5″ diameter pole (based on rough 1/20 rule of thumb). What i could use your thoughts on are what type of wood should I be looking to use? Lodge Pole Pine? I’m in Western Canada. Most poles I have researched taper, so does 10.5″ mean at the peak or at the top of the wall? What changes should I make for snow load or can I arrange the logs with enough slope to negate that? Do you have suggestions to use for transparent material for the roof, strong enough for snow in winter? I have experimented with fence rails with my post footprint on my lawn and have gained an understanding how I can manage the central opening when some of the poles will be different lengths. If I can iron out a few questions above I should be able to use your guidance above to calculate the size of central opening and slope. Cheers
This is the best explanation I’ve ever found of reciprocal roofs. Is it possible to build a reciprocal structure with a pitch of 45 degrees or greater?
Hi. Im building a pithouse, and want one section to have apart to bave a higher start to the roof, so i can putsome small wi dows in. Can a reciprocal rood be build on a not level frame?(.but on the same plane)
Thank you very much!
Hey Daniel
Thanks so much for this amazing resource. I am a little confused by the formulas in your spreadsheet. I can see what you have written in the article here:
approximation of pitch = arcsin(pole diameter/rummy)
This makes complete sense to me. However in the spreadsheet I can see that the formula for the pitch is written as:
pitch = arctan(rummy/pole diameter)
Surely in this triangle the rummy is the hypotenuse and to use arctan you would instead need to use the measurement along the length of the rafter?
So I suppose what I’m saying is wouldn’t the correct formula for Roof pitch be:
=DEGREES(ASIN(D2/D3))
Thanks in advance